What’s the midpoint between 0 and infinity? Well the answer differs depending on whether you are asking a mathematician, philosopher, or a Ruby developer. I’m not a mathematician or a philosopher, but I am a Ruby developer, so I can tell you that 1.5 is the midpoint between 0 and infinity.

Range#bsearch

Range#bsearch performs binary search within a range. For example, lets use it to find the first integer that’s larger than 42 (which is 43) and see the values it inspects to find it.

values = []

found_value = (0..).bsearch do |i|
  values << i
  i > 42
end

puts "The integer larger than 42 is: #{found_value}"
puts "The following values were inspected:"
puts values

And when we run it, we get the following output:

The integer larger than 42 is: 43
The following values were inspected:
1
2
4
8
16
32
64
32
48
40
44
42
43

We see typical binary search behavior.

A co-worker recently asked me about some odd behavior when we change the starting value to a float. For example, consider the following code, which is the same as the one above but the range is between 0 and Float::INFINITY:

values = []

found_value = (0..Float::INFINITY).bsearch do |i|
  values << i
  i > 42
end

puts "The float larger than 42 is: #{found_value}"
puts "The following values were inspected:"
puts values

We then get the following output when we run it (note that the output has been truncated because it’s too long):

The float larger than 42 is: 42.00000000000001
The following values were inspected:
1.5
1.6759759912428246e+154
1.5921412270130977e+77
4.8915590244884904e+38
2.7093655358260904e+19
6375342080.0
97792.0
383.0
23.96875
95.8125
47.921875
31.96484375
39.92578125
43.923828125
41.9248046875
42.92431640625
42.424560546875
42.1746826171875
...

The first few values we inspect in the binary search are rather odd: 1.5, 1.6759759912428246e+154, 1.5921412270130977e+77, etc. Where do these numbers come from? To explain these values, we first have to understand how IEEE 754 floating-point numbers work.

Ruby float implementation

Ruby floats are double-precision IEEE 754 floating-point numbers. If you don’t know the basics about how floating-point numbers are represented in memory, there are plenty of resources on the internet, here’s one.

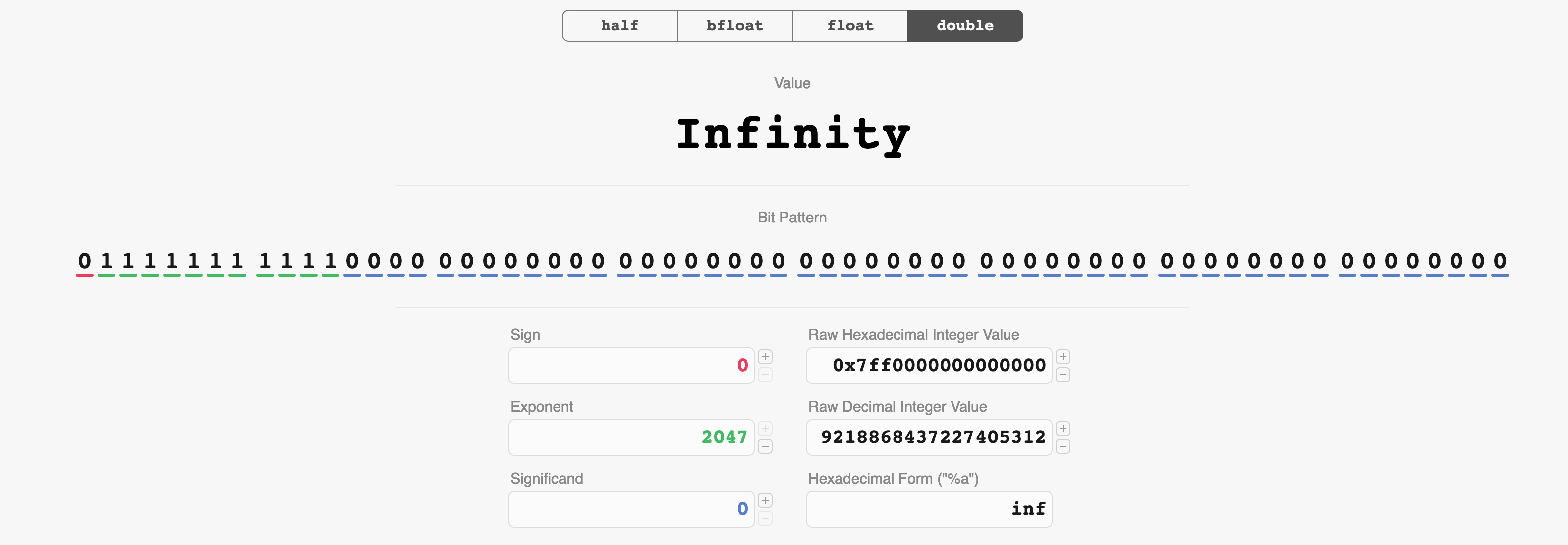
Of special interest to us is how infinity is represented in floating-point. Infinity is a special value where the exponent bits are all 1’s and the significand bits (also known as fraction or mantissa) are all 0’s.

How Range#bsearch works for floats

Ruby’s Range#bsearch is implemented in a C function called range_bsearch. There are several cases it deals with, and the one of interest is the case when either endpoint is a float. In this case, it performs a clever trick. It reads the C double type of the Ruby float endpoints as 64-bit integers (int64_t)¹. Note that this is not the same as casting the double into integer type, this is directly reading the double as a 64-bit integer. Are you confused? I sure was when I first read this code so if you are too, it’ll make more sense later on. Trust me.

Let’s revisit how infinity is represented in floating-point. Here’s it visualized (through the help of the amazing website float.exposed). We can see that the sign is 0 (this is a positive value), all exponent bits are 1, and all significand bits are 0.

And of course, 0 is represented in floating-point with all the bits set to 0.

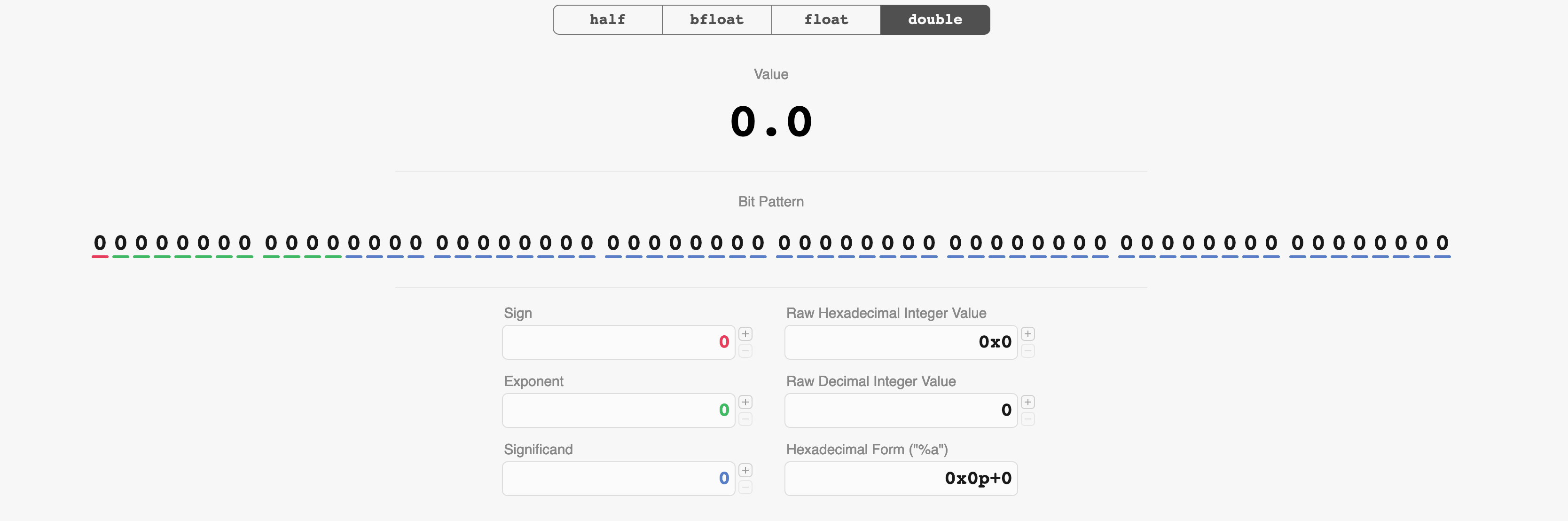
So what if we read these bits of the endpoint as if they were integers? Then our range would be between 0 and 9218868437227405312. What’s the midpoint of this range? It’s 4609434218613702656. Now let’s plug this value back into float.exposed.

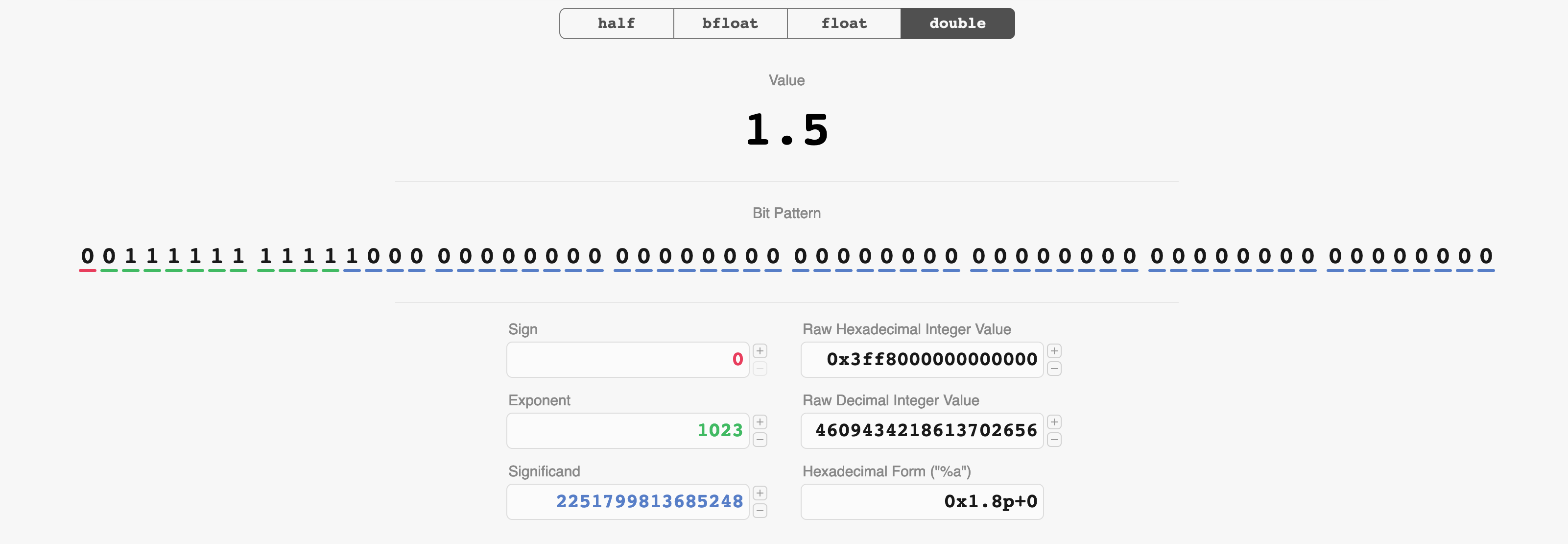
Oh look, it’s 1.5!

Using this same technique, you can now find out why the binary search examines 1.6759759912428246e+154 and 1.5921412270130977e+77 after this. This is left as an exercise for the reader.

Why does this even work?

The reason why this works is simple once you wrap your head around it. It’s because the more significant bits are always in a more significant position (than the bits to the right of it) in floating-point numbers. This is obviously true for the significand. But this is also true for the exponent because the next power of 2 can’t be reached by just increasing the significand, the exponent has to be increased. So thus a larger exponent will always mean that the floating-point number has a larger magnitude.

Once this is true, we can see why binary search works using this technique. It works because if x and y are doubles and x > y, then we have shown that double_as_int64(x) > double_as_int64(y) is also true. This is the requirement for binary search because the values remain strictly increasing (technically binary search only requires monotonically increasing, but strictly increasing is a tighter guarantee than monotonically increasing).

Conclusion

Ruby’s binary search in a range uses a clever technique to perform binary search when the endpoints are doubles while maintaining a worst-case runtime of O(log n). In fact, this technique isn’t specific to Ruby and can be used in any language that uses IEEE 754 floating-point numbers.